【人気ダウンロード！】 ��形 弧の長さ 公式 中学 133097-扇形 弧の長さ 公式 中学

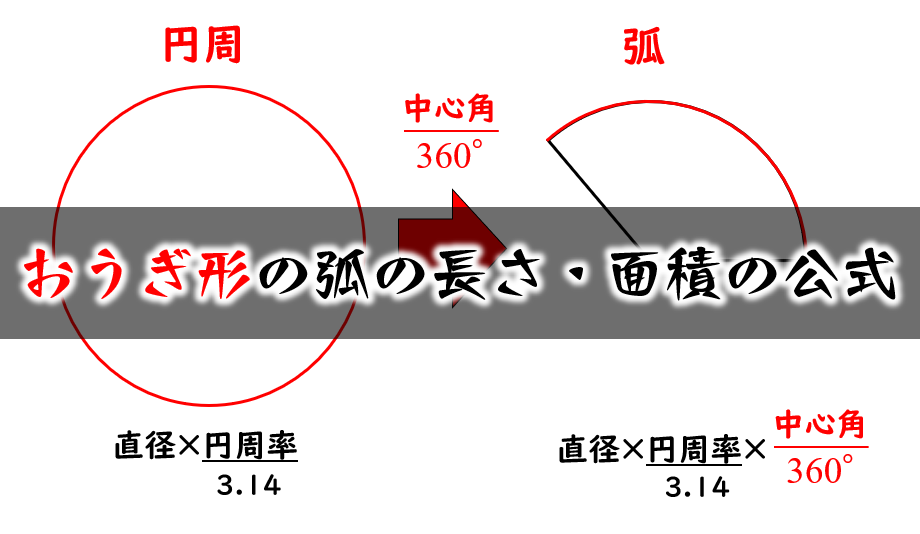
扇（おうぎ）形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を 円の公式 円周・面積 円周率 = 3．14 円周の長さ = 直径 × 円周率 円周率 ＝ 円周 ÷ 直径 おうぎ形の弧の長さ ＝ 直径 × 314 × 中心角 ÷ 360 円の面積 ＝ 半径 × 半径 × 円周率 弧の面積 ＝ 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 円周の長さ 重要 円周率とは、「直径」を何倍したら「円周 扇形の周の長さとは、扇形を1周した長さのことをいうので、次のように求めることができます。 つまり！ 弧の長さを求めて、半径を2個分出せばOKということです。 なんだ！ 単純だね♪ では、弧の長さの求め方を確認した上で問題を解いてみましょう。

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

扇形 弧の長さ 公式 中学

扇形 弧の長さ 公式 中学-扇形の部分が円の「何分の1」なのかがわかれば簡単に解くことができます。 つまり、円は360度なので、扇形の中心の角度がわかれば以下のような公式に当てはめるだけで問題を解くことができます。 おうぎ形の弧の長さ ＝ 直径 × 円周率 × 中心角 ÷ 360 円・扇形の公式まとめ 円周： 2πr 2 π r 円の面積： πr2 π r 2 扇形の弧の長さ： 2πr× a 360 2 π r × a 360 扇形の面積： πr2 × a 360 π r 2 × a 360 扇形の面積（弧の長さ l l からの導出）： 1 2lr 1 2 l r ※半径： r r 、円周率： π π 、中心角： a a 、扇形の弧の長さ

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

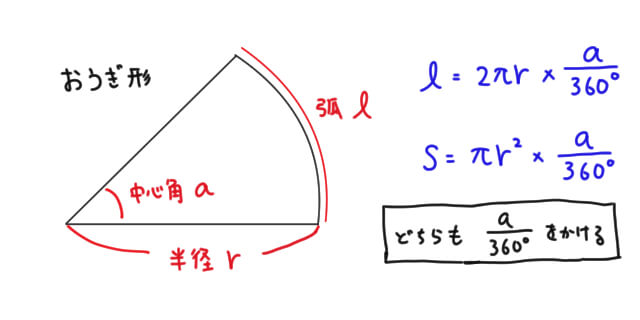
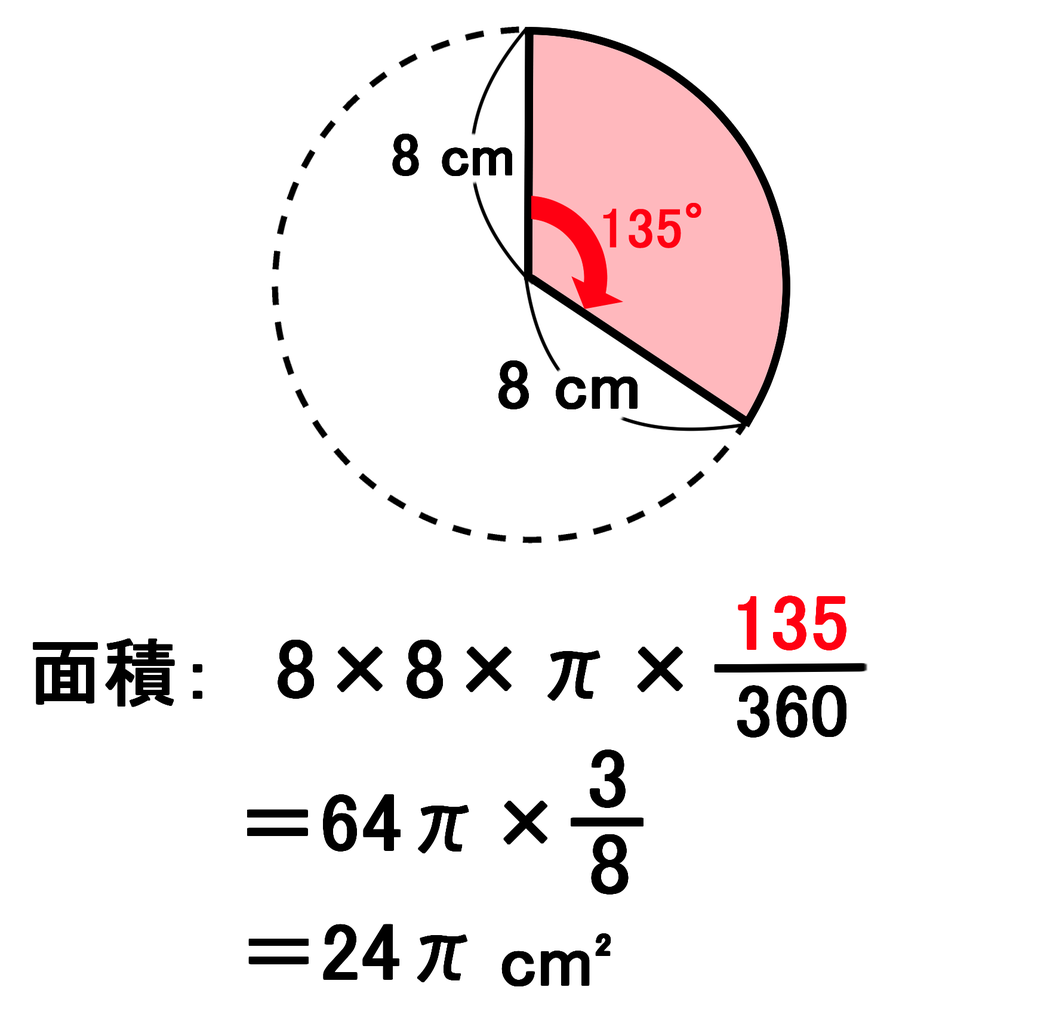
おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の扇形の弧の長さ L=rθ 扇形の面積 S＝r^2θ/2＝rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は？1分でわかる意味、公式、求め方、ラジアンとの関係 扇形の弧の長さと 中学数学「おうぎ形の孤の長さと面積」がどうしても理解できないという子にも分かるように、ひとつひとつのつまずきポイントを丁寧に解説していくよ！ 弧の長さの公式：\(l＝2πr×\frac{a}{360}\) おうぎ形の面積の公式：\(s＝πr^2×\frac{a}{360}\) ABOUT ME

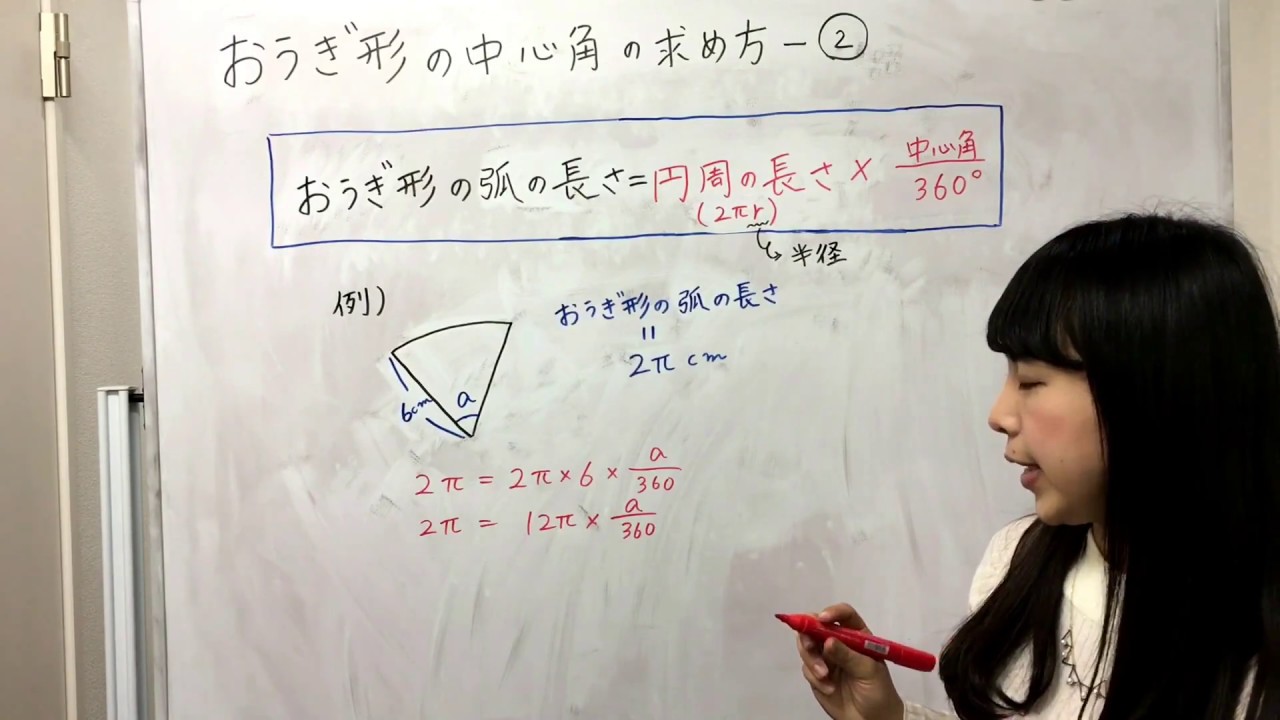
扇形 ～弧の長さ、半径から中心角を求める～ 作者 Enpitsu さん 実行数 扇形 ～弧の長さ、半径から中心角を求める～ 作者 扇形の面積 ＝ 弧の長さ × 半径 ÷ 2 なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。 では、どうしてこのようなことがいえるかを考えて見ましょう。 扇形の面積を求める公式は前に述べたとおり以下の公式です。 扇形の という公式が得られる。 次に周りの長さについての証明をします。 半径 cm,中心角90 の弧の長さを求めると, 半径 cm, 中心角180 の弧の長さを求めると, となり、周りの長さは次式で考えられる。 (周りの長さ) よって, (周りの長さ) (cm)という公式が得られる。

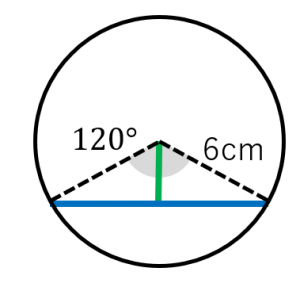
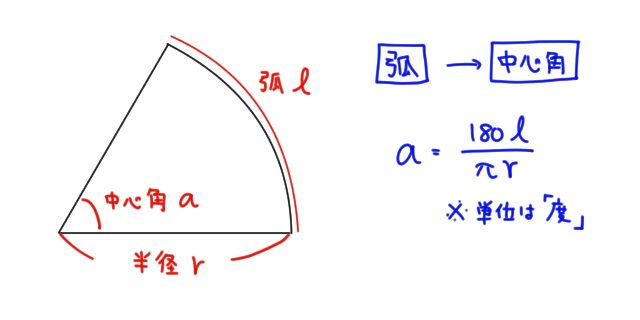
答え おうぎ形の面積が与えられているので こちらの公式を利用します。 まずは、半径9㎝の円の面積を求めます。 そして、公式にそれぞれの値をあてはめていくと 約分をしていきましょう。 (πも約分で消えてしまいます) （2）半径 ㎝、弧の長さ cmの問題文に、弧の長さと中心角が与えられていて これをヒントに半径を求めろというわけです。 この問題のポイントは 半径を x として、方程式を作って解く！ 弧の長さが与えられているので 弧の長さの公式に x 、数を当てはめていきましょう。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。

中１ 数学 中１ ７４ おうぎ形の弧と面積 Youtube

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

 おうぎ形（扇形）の半径と中心角を入力すると、その面積、弧の長さ、周囲の長さ、弦の長さが出力されます。中心角は 0 〜 360 までの値を入れてください。度（°）の記号は不要です。数字は半角のみ。 2分でわかる！扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね？？ それじゃあ、 扇形の弧の長さの公式 をみていこう！ 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。その通りです！ ではここで1度，おうぎ形の弧の長さの公式を確認しておきましょう💡 おうぎ形の弧の長さの公式 半径r，中心角a°のおうぎ形の弧の長さをℓとすると，次の式が成り立つ。 生徒 そうすると，問題のおうぎ形はr=9，ℓ=6πということ

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

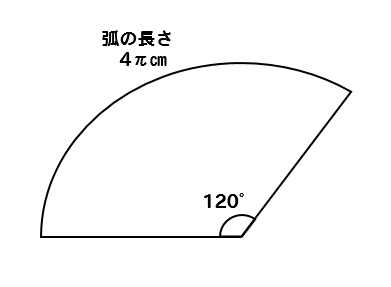
 扇形のまわりの長さは、 扇形の弧の長さ＋半径×2 で求められます。 この扇形の弧の長さ＝18×314× ＝14（cm） よって、求める扇形のまわりの長さは 14＋9×2＝3684（cm） 答え 3684㎝ ～平面図形の面積・まわりの長さを求める公式まとめ～ 円の面積扇形の弧の長さと面積 平面図形 公式集 確認シート a ＝長さ b ＝長さ h ＝高さ ℓ ＝弧の長さ S ＝面積 V ＝体積扇形の面積と弧の長さがわかっているときの、扇形の角度の求め方を教えてください。 〔回答〕 以下の説明において、 S＝おうぎ形の面積，ℓ＝弧の長さ，r＝おうぎ形の半径，x＝中心角の大きさ とします。 まず、おうぎ形の面積に関しては （1

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張

 扇形の公式はこう変わる 弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, と導け, 扇形の面積 は, 度数法の公式 をradに置き換えて, また, 扇形の弧の長さの公式より21年12月15日 このページは、 中学1年生で習う「おうぎ形の孤の面積を求める問題集」が無料でダウンロードできる ページです。 この問題のポイント ・おうぎ形の孤の面積は、次の公式を使って求めることができます。 おうぎ形の半径をr、中心角をaと平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 折り目の作図 最短経路の作図 おうぎ形_半径と中心角から弧の長さや,面積を求める

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

円とおうぎ形 応用 無料で使える中学学習プリント

扇形の弧の長さと面積の求め方としては、どのように計算すればいいのでしょうか。 扇形の弧の長さや面積を計算する場合、必 続きを読む 扇形 弧の長さ 公式 中学 扇形に関する問題孤の長さ、面積は何年生で習いましたか？ 文部省の指導要綱には中学1年生のところにありました 扇形の弧の長さの公式がなぜ 2πr×中心角÷360となるのか理解 できま扇形の弧の長さと面積を出すためには、その前に円周と面積を必ず出さなければいけません。 そのため、小学校の算数のおさらいをしましょう。 円周や面積については、以下の公式によって計算します。 円周 ＝ 直径 × 314（円周率） 円の面積 ＝ 半径

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

円 扇形 の面積 周や弧の長さの公式 数学fun

 中学数学の扇形の中心角と弧の長さについて質問です。 問題は 図のような半径が3cmの円oがある。線分abは点aにおける円oの接線で、ab＝3cmである。 線分obと円周との交点をcとし、点bから線分acの延長上にひいた垂線と線分acの延長との交点をdとする。 これには公式があります。 半径×弧の長さ÷2で求められます。 なので、下の問題も・・・ 8cm×7cm÷2=28cm² となります。 簡単ですね！ でも、コレで終わってはダメです。 なぜそうなるのか？を知っておくことが大事。 この公式自体は有名（？）です。 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね

扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

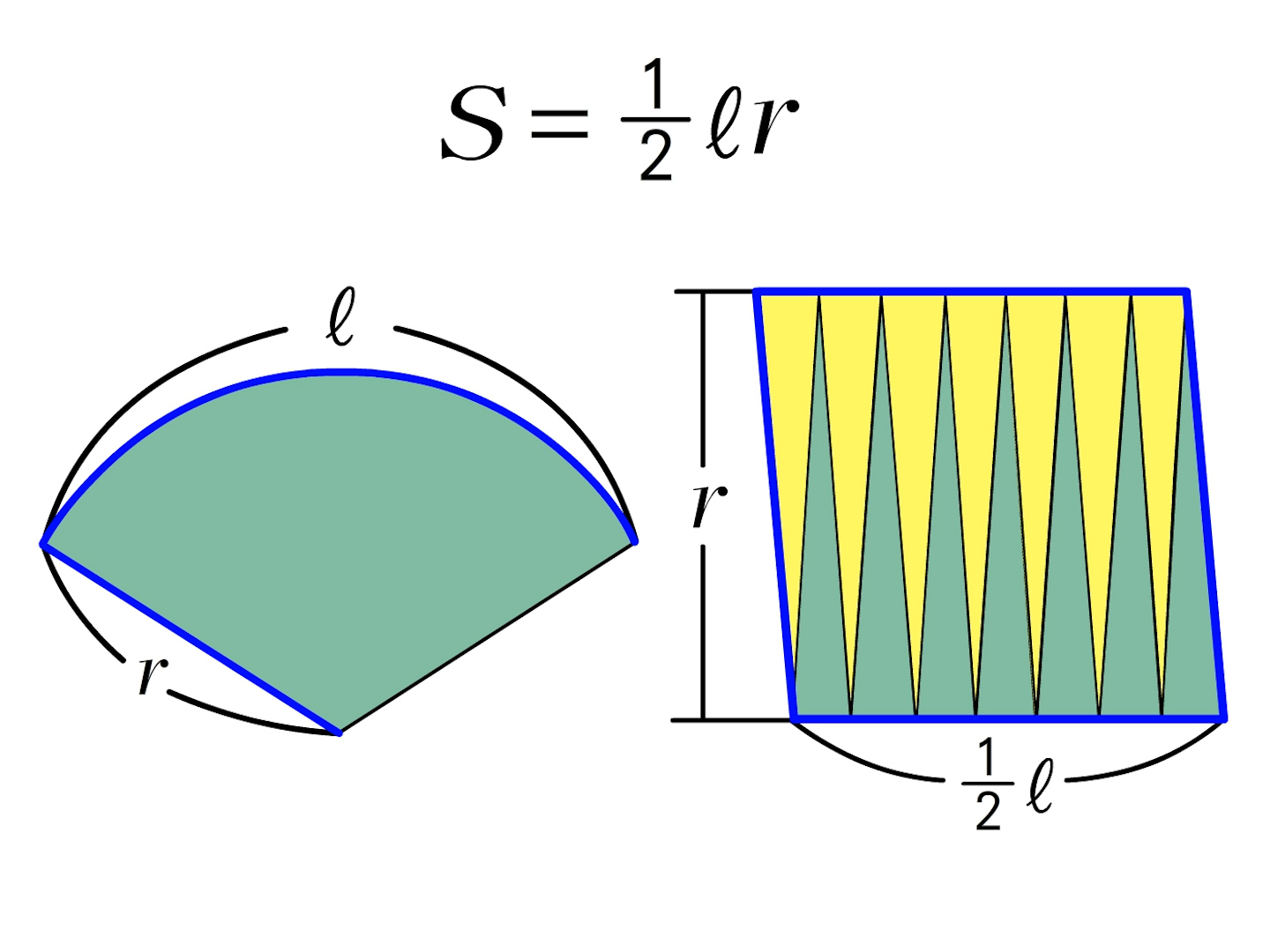
 扇形の面積・弧の長さ 計算機 かんたん計算機 かんたん計算機 シェアする 「ご注意計算結果について、正確な結果が出るように検証をしていますが、間違いがある可能性もあります。 ご了承ください。 扇形の弧の長さ 底面の円の円周と等しく、2rπ 中学数学 2次方程式の解の公式を導出する ( 平方完成 ) 中学数学 正負の数 負数を減算するってどういうこと？ ( マイナスのマイナを考えていきたいと思います。 この公式のポイント ・ おうぎ形の面積は「1／2×弧の長さ×半径」 で求めることができます。 ・おうぎ形の半径をr、弧の長さをLとしたとき、面積Sは下の公式で書くことができます。 S = 1 2 l r ぴよ校長 おうぎ形は、半径

扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

 まずは、求めたい半径の大きさを ㎝とします。 すると、半径 ㎝で中心角1°の扇形の弧の長さは と表すことができます。 そして、弧の長さが ㎝になるはずだから という方程式が完成します。 あとは、これを解いていけば の値（半径）を求めることが中学校1年の数学で習う「扇形の弧の長さと面積」の問題集です。 問題の数値はランダムで生成することができ、答えの表示・非表示も切り替えられます。 印刷してご活用ください。 ちなみに扇形の基本的な公式や問題の解き方について詳しい解説は

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

扇形の面積の求め方 公式と計算例

中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ

1

おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ

円 扇形 の面積 周や弧の長さの公式 数学fun

公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ

中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube

平面図形の面積の求め方 基本編 中学受験 塾なし の

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学

扇形の弧の長さの求め方 公式と計算例

おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ

中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ

扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

1

なぜ おうぎ形の面積は１ ２ 弧の長さ 半径 なのか を説明します おかわりドリル

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

円 扇形 の面積 周や弧の長さの公式 数学fun

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun

おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト

扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強

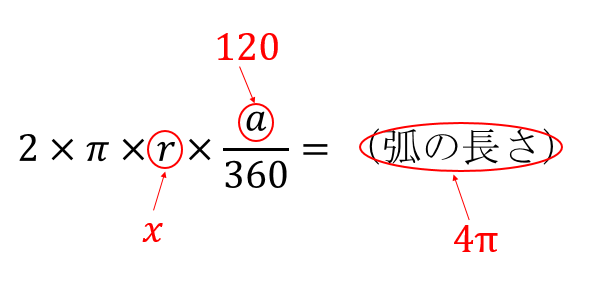
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

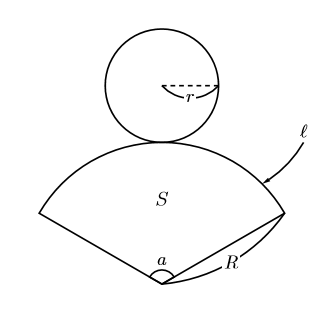
中学数学 円錐関連の公式の導出 数樂管理人のブログ

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

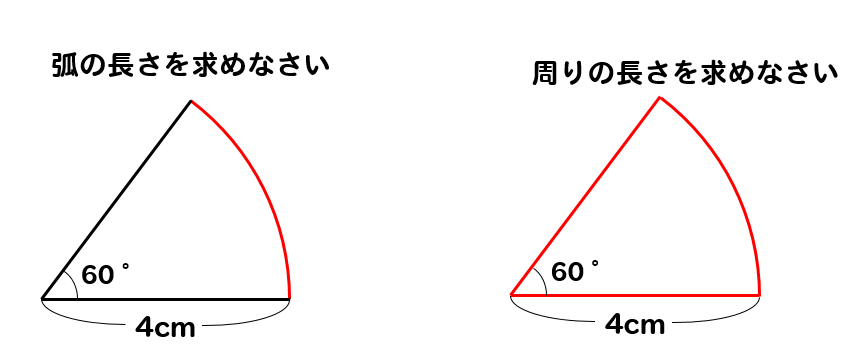
おうぎ形 注意 周りの長さを求める公式を解説 数スタ

扇形の中心角の求め方を教えてください 中心角の求め方は２通りのパタ Yahoo 知恵袋

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

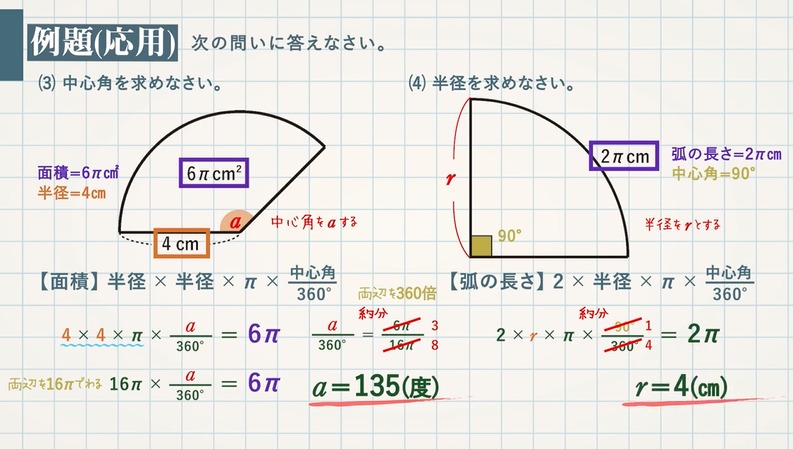
おうぎ形まとめ 弧と面積の求め方 教遊者

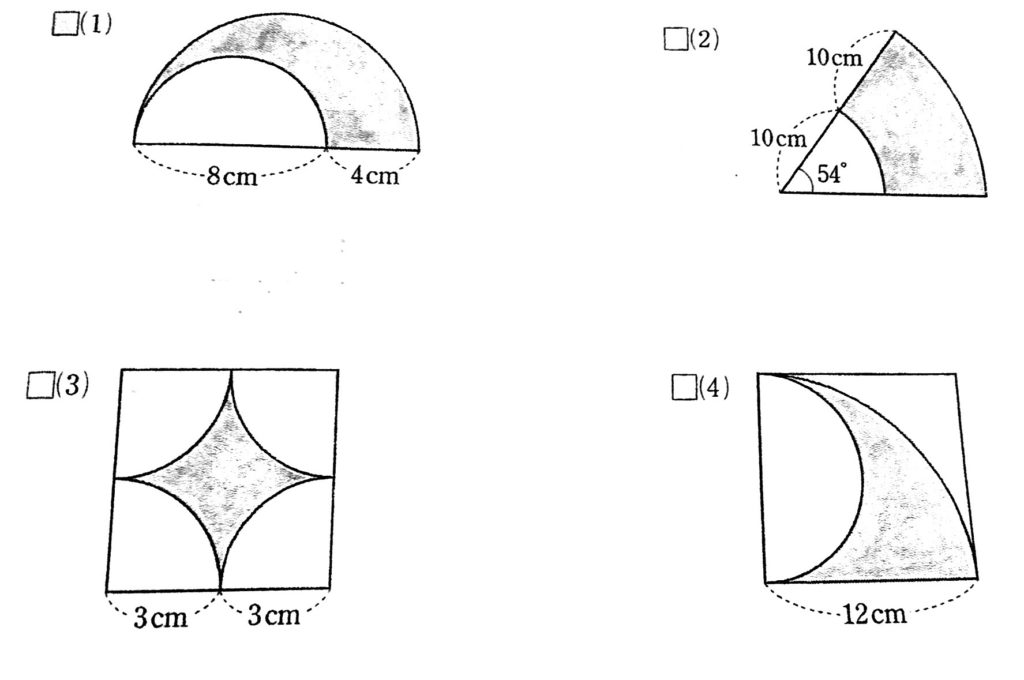
無料 中１数学 標準問題 解答プリント 138 平面図形５ おうぎ形の弧と面積

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

1

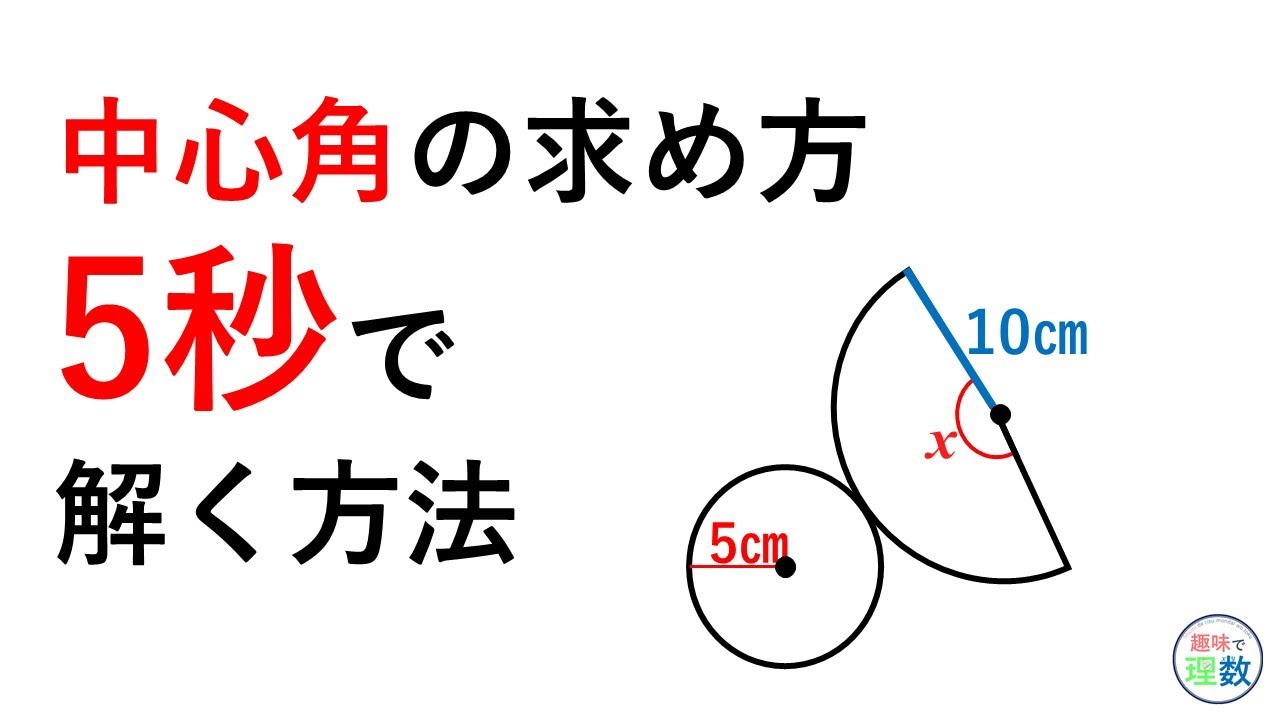
おうぎ形の中心角の求め方 Youtube

弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学

おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学

受験数学かずスクール 扇形の弧の長さと面積

公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

おうぎ形の弧の長さと面積 中学数学 平面図形 １ Youtube

おうぎ形 注意 周りの長さを求める公式を解説 数スタ

扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強

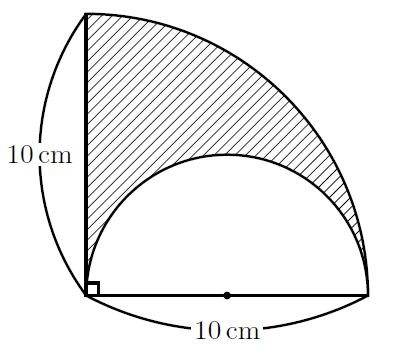
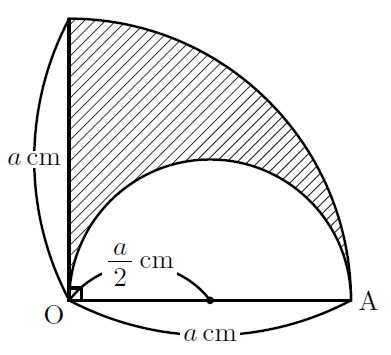
標準 おうぎ形と正方形の面積 なかけんの数学ノート

中心角40度 弧の長さ２pｃｍの扇形の面積中心角３０度 弧の長さpｃｍの扇形 Yahoo 知恵袋

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

1年 おうぎ形の面積 数学イメージ動画集 大日本図書

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

扇形の弧の長さと面積 計算ドリル 問題集 数学fun

扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト

扇形の弧の長さの求め方 公式と計算例

扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学

中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円 扇形 の面積 周や弧の長さの公式 数学fun

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

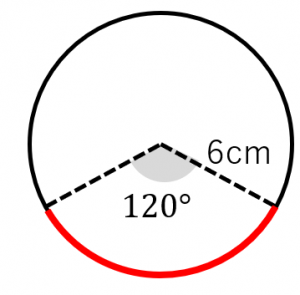
弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

おうぎ形の面積 弧度法との関連から眺める 身勝手な主張

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ

裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 ２ Youtube

おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に

表面積の問題で 中心角の求め方が分からず答えを見たんですが 説明文の意味がわ Clearnote

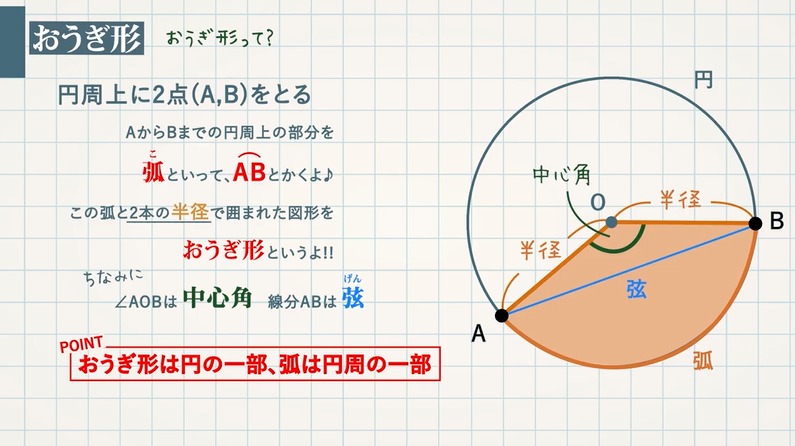
おうぎ形まとめ 弧と面積の求め方 教遊者

円柱の表面積の求め方

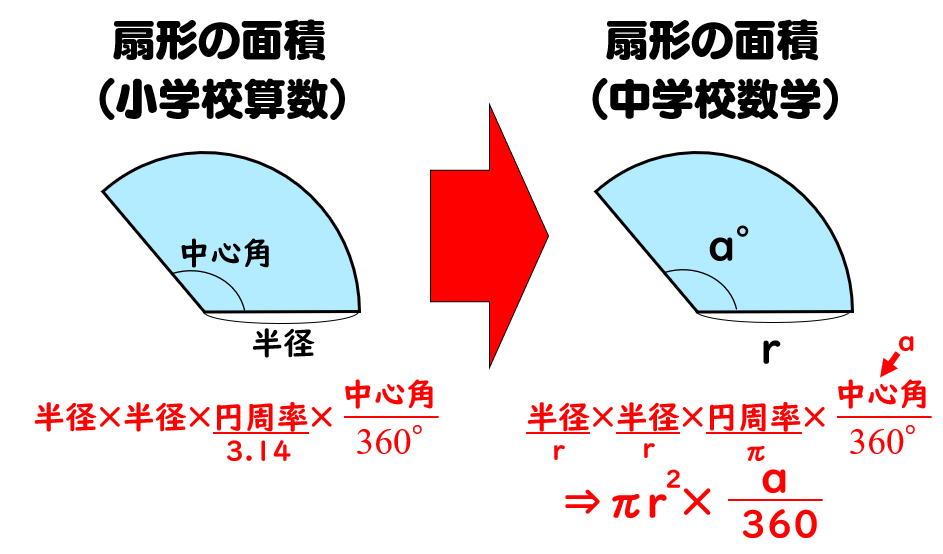
円 扇形 の面積 周や弧の長さの公式 数学fun

扇 おうぎ 形の面積を求める公式と弧の長さの求め方

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Incoming Term: 扇形 弧の長さ 公式 中学,